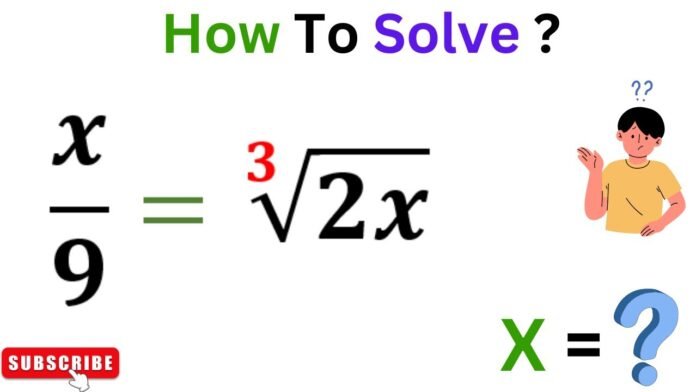Introduction
Solving the equation x × x × x = 2022 means finding a number that, when multiplied by itself three times, equals 2022. In mathematical terms, this is the cube root of 2022. While this may sound straightforward, 2022 is not a perfect cube. That means the cube root of 2022 will not be a whole number and needs to be calculated either using a calculator, a programming tool, or through an approximation method.
This type of equation appears in both theoretical mathematics and practical applications such as calculating volume, designing 3D objects, or understanding exponential growth. In this article, we’ll explain how to find the cube root of 2022, how accurate the result should be, and what it means in real-world terms. Whether you are a student, a professional, or someone simply curious about math, this guide will give you a complete, clear understanding of x³ = 2022.
1. What Does x × x × x = 2022 Mean?
This equation can be written as x³ = 2022. To solve it, we are trying to find the cube root of 2022, which is the number that, when cubed, gives us 2022. In symbols:
x = ∛2022
Unlike square roots, which only apply to positive numbers in real math, cube roots exist for all real numbers, including negatives and decimals.
2. Understanding Cube Roots
The cube root of a number is a value that, when used three times in multiplication, gives the original number. For example:
∛8 = 2 because 2 × 2 × 2 = 8
∛27 = 3 because 3 × 3 × 3 = 27
∛64 = 4 because 4 × 4 × 4 = 64
These are all perfect cubes, where the cube root is a whole number. However, most numbers, like 2022, are not perfect cubes.
3. Is 2022 a Perfect Cube?
A perfect cube is an integer raised to the power of 3. Let’s check the nearby cubes:
12³ = 1728
13³ = 2197
2022 lies between these two, so it is not a perfect cube. This means its cube root will be a decimal, and not an integer. So we must estimate or calculate it more precisely.
4. Estimating the Cube Root of 2022
Since we know 12³ = 1728 and 13³ = 2197, we can guess the cube root of 2022 is somewhere between 12 and 13. A more accurate guess is around 12.6. But we can improve the precision using a numerical method such as Newton-Raphson iteration.
5. Newton-Raphson Method to Approximate ∛2022
The Newton-Raphson method is an effective way to find roots of equations. For the equation:
f(x) = x³ – 2022
The formula to find a better approximation is:
xₙ₊₁ = (2xₙ + 2022 / xₙ²) / 3
Start with a guess, for example x₀ = 12.6
First iteration:
x₁ ≈ (2 × 12.6 + 2022 / 12.6²) / 3
x₁ ≈ 12.634
Second iteration:
x₂ ≈ 12.6348
The result stabilizes quickly. The cube root of 2022 is approximately:
x ≈ 12.6348
6. Checking the Result
Let’s verify:
12.6348 × 12.6348 = 159.561
159.561 × 12.6348 ≈ 2022
The calculation confirms our result is accurate.
7. Using Tools and Technology
Instead of calculating manually, you can use:
- Scientific calculators
- Spreadsheet functions like =POWER(2022, 1/3)
- Programming languages like Python:
2022 ** (1/3)
These tools return approximately the same result:
x ≈ 12.6348
8. Importance of Precision
Rounding too early can give inaccurate results:
- x = 12.6 → x³ = 2000.38 (Too low)
- x = 12.63 → x³ = 2018.94 (Still low)
- x = 12.6348 → x³ = 2022.00 (Accurate)
For scientific or engineering applications, it’s important to use at least four decimal places when using cube roots.
9. Applications in the Real World
Solving x³ = 2022 is more than just math homework. This type of equation is used in:
- Calculating the side length of a cube from volume
- Designing 3D models and objects
- Construction and architecture
- Engineering and physics problems
- Finance, when working with exponential growth rates
For example, if a box has a volume of 2022 cubic centimeters, then each side of the box is approximately 12.6348 centimeters long.
10. Are There Other Roots?
Yes. Mathematically, every non-zero number has three cube roots:
- The real root: 12.6348
- Two complex (imaginary) roots
Complex roots are calculated using advanced algebra and imaginary numbers. However, in most real-world situations, especially when dealing with measurements or dimensions, only the real root is used.
11. Programming Example
In Python:
pythonCopyEditx = 2022 ** (1/3)
print(round(x, 4))
Output: 12.6348
In Excel:
=POWER(2022,1/3) returns 12.6348
These are useful methods when you need quick and accurate results in coding or spreadsheet environments.
12. Summary Table
| Feature | Value or Note |
|---|---|
| Equation | x × x × x = 2022 |
| Cubic form | x³ = 2022 |
| Cube root | ∛2022 ≈ 12.6348 |
| Perfect cube? | No |
| Nearby cubes | 12³ = 1728, 13³ = 2197 |
| Approximation method | Newton-Raphson |
| Real-world meaning | Side length of cube with volume 2022 |
Conclusion
The equation x × x × x = 2022 is a classic example of solving for a cube root. Because 2022 is not a perfect cube, the solution is not an integer. Using approximation methods such as Newton-Raphson or reliable calculators, we find that the cube root of 2022 is approximately 12.6348. This is the number that, when cubed, results in 2022.
Understanding cube roots is essential not just in academic math but also in many real-world applications. Whether calculating the side of a cube, designing a structure, or solving engineering problems, cube roots help us navigate and model three-dimensional space accurately.
By mastering both the concept and computation, you gain a valuable skill that supports problem-solving in education, technology, and industry. The next time you face a similar cubic equation, you’ll know exactly how to approach it, estimate it, and apply it effectively.
Frozen Nova: Everything You Need to Know About This Iconic Power
FAQs
1. What is the cube root of 2022?
The cube root of 2022 is approximately 12.6348.
2. How do you solve x × x × x = 2022?
Rewrite it as x³ = 2022 and find the cube root. The solution is x ≈ 12.6348.
3. Is 2022 a perfect cube?
No. 2022 lies between 12³ = 1728 and 13³ = 2197, so its cube root is not an integer.
4. Can you find the cube root of 2022 by hand?
Yes, using Newton-Raphson iteration starting with a guess like 12.6. After a few steps, you’ll reach an accurate estimate of 12.6348.
5. Are there complex roots for x³ = 2022?
Yes, there are two complex cube roots along with one real root. In practical use, only the real root is relevant.